当前位置：首页>石家庄>【难】2025-2026石家庄四十三中九年级期末数学试卷及压轴题解析.

【难】2025-2026石家庄四十三中九年级期末数学试卷及压轴题解析.

  • 2026-02-07 10:00:16
【难】2025-2026石家庄四十三中九年级期末数学试卷及压轴题解析.
选择压轴题第12题
解：
题型分析：折叠+隐形圆最值问题
①有折叠性质知：对应点的连线被对称轴（折痕）垂直平分，可得∠AFD=90°。
②最值就是构造三角形，最值遇到直角三角形往往取中点构造。
故取AD中点T，连接CT，当点C，F，T三点共线时，CF最小，计算结果如上图所示。
填空题第16题
解：
题型分析：一定一动直线型瓜豆原理。几何原理是旋转性质
点P在AH上运动，意味着AH上的每一个点都绕着点Q逆时针旋转90度得到点N，两点确定一条直线，只需要让点P取两个特殊位置，即可画出点N的运动轨迹，如下图所示：
具体位置计算
故：1/2≤t≤25/8
解答题第22题：我们只研究最后一问
题型分析：切线最值问题
如图：MP始终与OD垂直，则∠MPC的角度始终不变，当MP与圆相切时CP最大！，计算结果如上图所示,利用外角导角和切线长定理可计算。
解答题第23题：我们只研究最后一问
题型分析：动函数与整点问题，此类问题关键点有两个，一是抓住运动中的不变量，二是整点问题先把可能的点描出来，再进行分析判段。
解：易知二次函数开口不变，且始终关于x=1.5对称，所以，当n=2,即有两个整点时，必然是坐标轴上两个关于对称轴对称的点，点（1,0）和点（2，0）。具体计算如下图。
当n=8时，顺着n=2时的情况，函数要向上移动，我们把可能出现的一些点标出来，如下图所示：
先验证C=0时，此时显然不满足，当C＜0，即将函数向下平移时，不难发现满足条件。
综合评价：这类动函数整点问题难度比较大，需要扎实的函数功底和画图分析能力。
压轴题第24题：还是只研究最后一问
题型分析：此题没看出最后一问啥模型，就是三角函数解型题，需要锐角三角函数掌握的比较好，当然知道“12345”模型提升解题速度
上图即为：“12345”模型及证明方法
分类讨论：情况①
情况②（这一种情况导出∠DPT=β，发现只有sinβ变了，其余式子没变，直接代入①计算即可）
【1】先导角
【2】确定底和高，我选择的是PE当底
【3】利用三角函数计算，注意sin∠PAH,这一步选择设而不求！
【4】最后就是计算和考虑取舍问题。
【压轴问综合评价】暴力计算对初中生来说挑战性很大，所以在河北中考中往往是压轴问，对于学过高中解三角形的同学来说问题应该不大，属于在中考中为满分选手准备的题型。
最后建议河北中考学子多关注石家庄43中的考试题，质量很高。

往期文章精选

2025保定一中1+3数学压轴题一题六法---初一可做
【福利】2023保定一中1+3入学测试题（回忆版）
2024保定市1+3考试真题汇总（含解析）
保定1+3备考中学生最容易忽视的一类几何证明题（勾股定理的应用）
【自招专题】因式分解证明乘法公式
【加权逆等线旋转中心的找法】2025-2026石家庄四十三中九上二阶数学压轴题深度探究
[备考1+3]曼哈顿距离解2025保定一中1+3升学考试中的压轴题[高中生也要掌握]
【海盗埋宝？】2025-2026石家庄四十三中八年级上期中数学压轴题解析
特殊角处理策略2025石家庄一模22题最后一问解答
2025石家庄中考数学一模压轴题解法分享
再见手拉手---2025邯郸一模压轴题解法分享（含试卷及答案）
【河北新中考】2025河北中考数学样卷全科样卷下载

河北特色中考：点动成线

定角定积---反演变换

圆幂定理在河北中考中的应用

反比函数与线段交点：一瞬的相遇，一世的离歌

河北中考新纪元，30°角定天弦---对2022河北中考压轴题的深度剖析

2022河北中考考点预测1：海盗埋宝

二次函数与线段交点：由动思静，另辟蹊径。

平面几何中的老六---建系法破解2022河北各市一模压轴题

从盘古开天，到新冠肺炎---一文搞定切线最值在河北中考中的应用

从入门到精通，定比分点公式解2023河北中考压轴题

河北中考：参变全分离、半分离、不分离

手拉手的妙用---对2025河北中考样卷24题的深入剖析

保定1+3备考中学生最容易忽视的一类几何证明题（勾股定理的应用）

瓜豆原理的应用---2025石家庄48中一模压轴题解析

【数学跨学科物理】离物理很近，离数学很远---解2025南京金中集团中考零模数学填空压轴题

2025河北中考二次函数怎么考---对2025河北中考样卷23题的深入剖析

河北特色中考：线过定点到点动成线---对2025莲池区八上期末试卷核心题深度剖析。

圆幂定理在河北中考中的应用

2025保定莲池区中考数学一模测试卷及解析

保定1+3备考中学生最容易忽视的一类几何证明题（勾股定理的应用）

瓜豆原理的应用---2025石家庄48中一模压轴题解析

将军巡营费马点的应用及拓展—对2025石家庄40中八下期中数学压轴题的深入探究

圆的第二定义解2025河北中考模拟（解密二）压轴题
手拉手模型学生又帮我总结了个新结论
浅谈押中考题的思路附两道原创好题。

瓜豆原理秒杀2025张家口桥东区模拟T16压轴题

从小初高数学到初中物理方法解透三角形中线段比问题
【二次函数怎么考】齐次化思想在中考中的应用
2025乐凯初二数学月考压轴题解析
2026年1月保定莲池区九年级数学期末试卷及解析
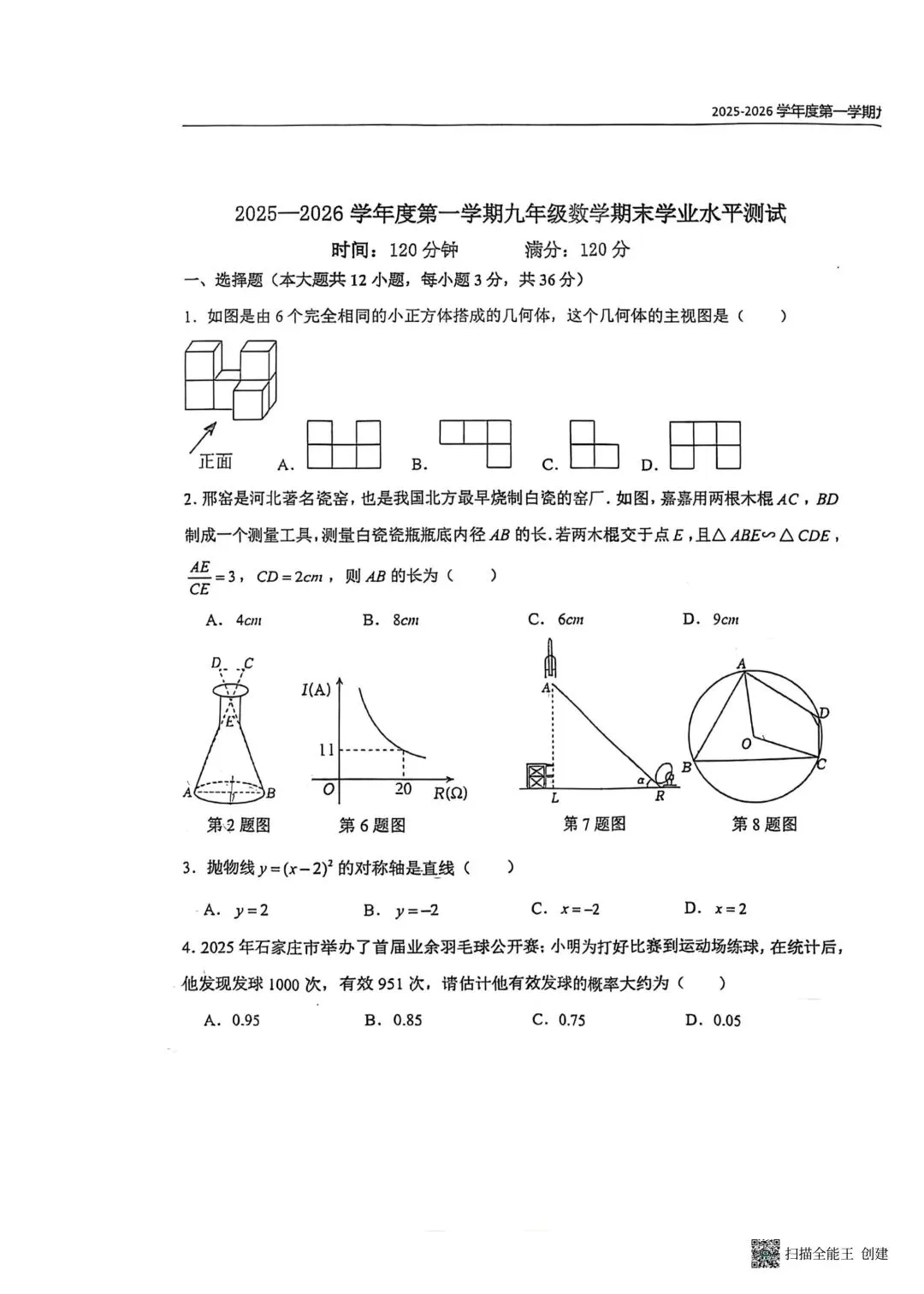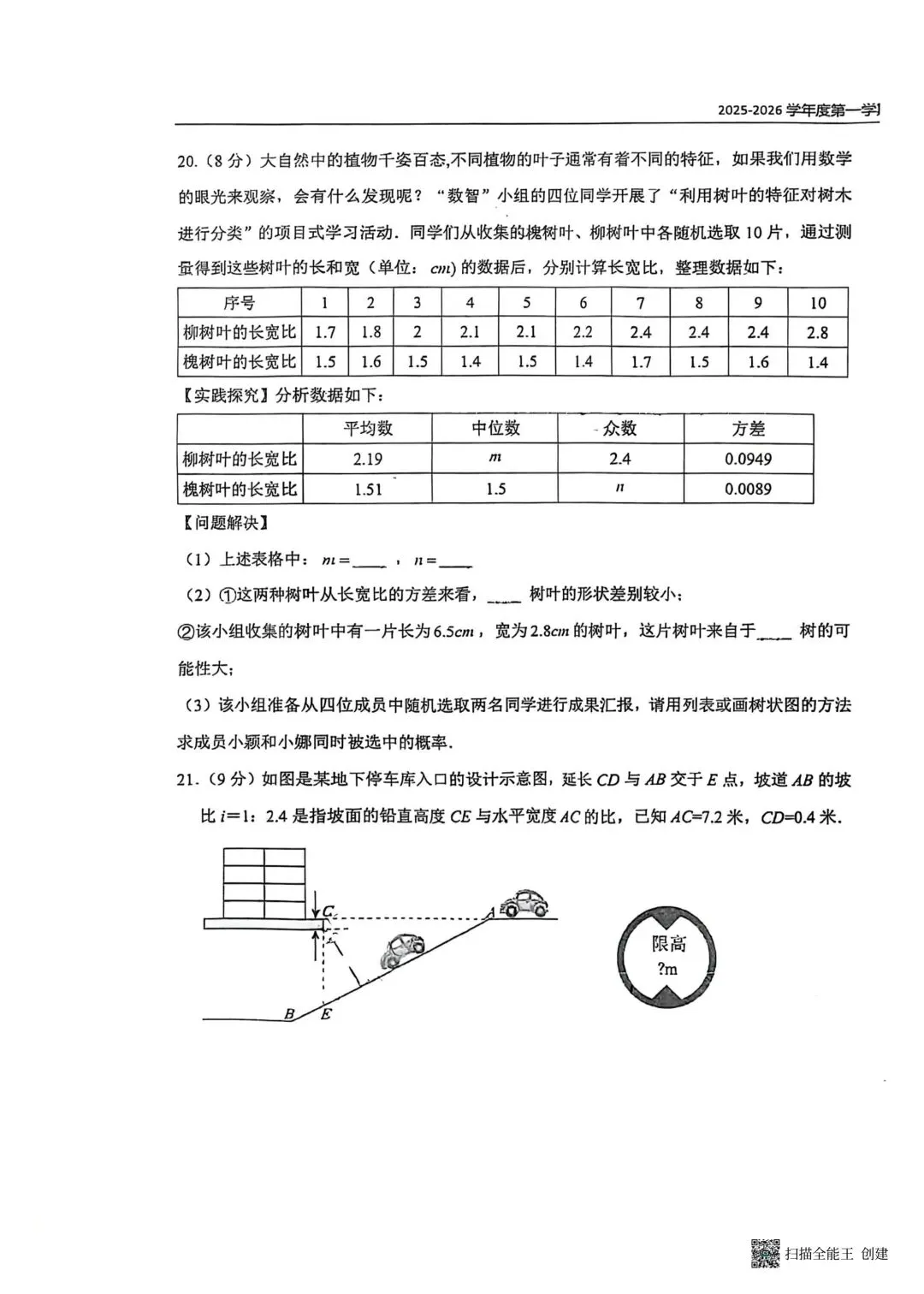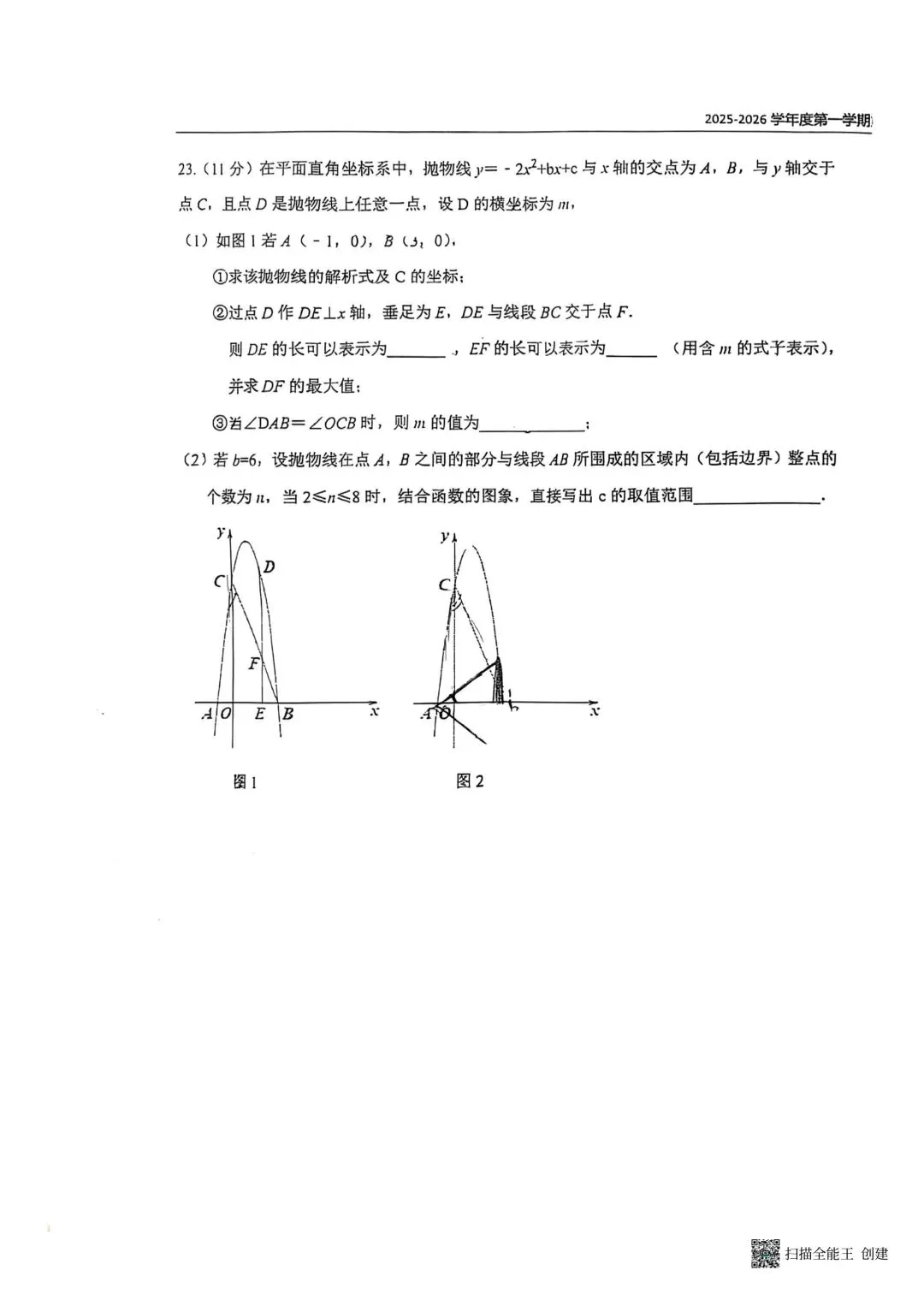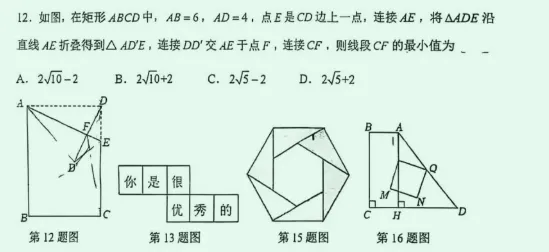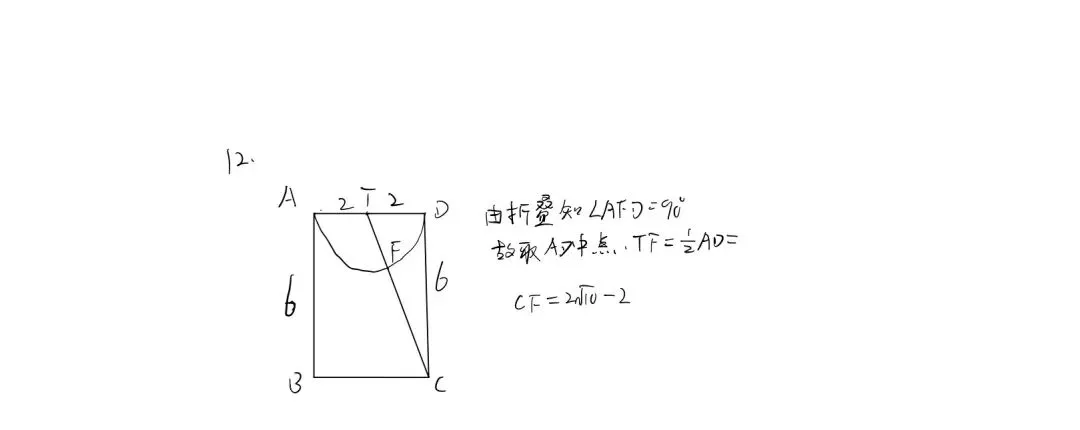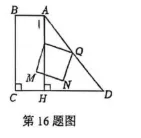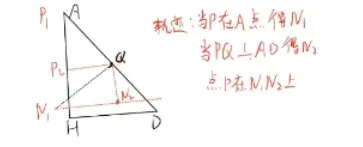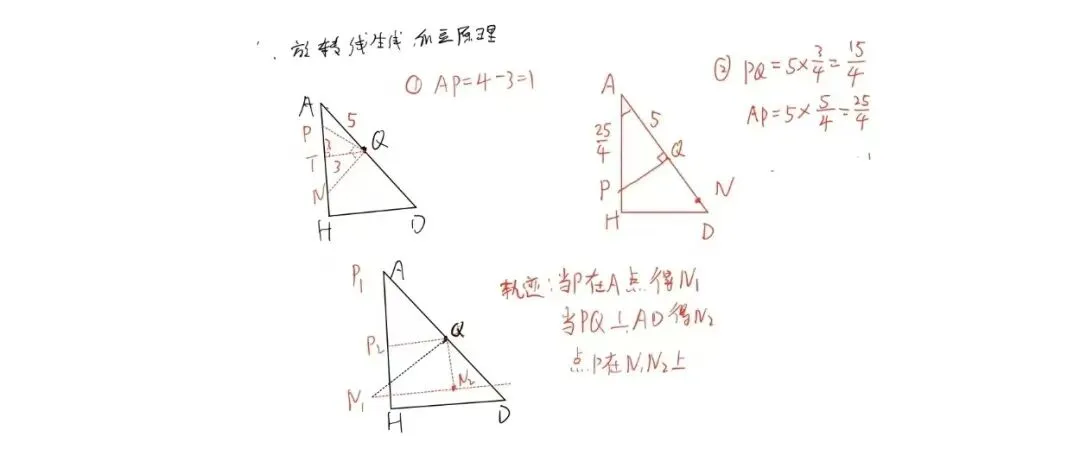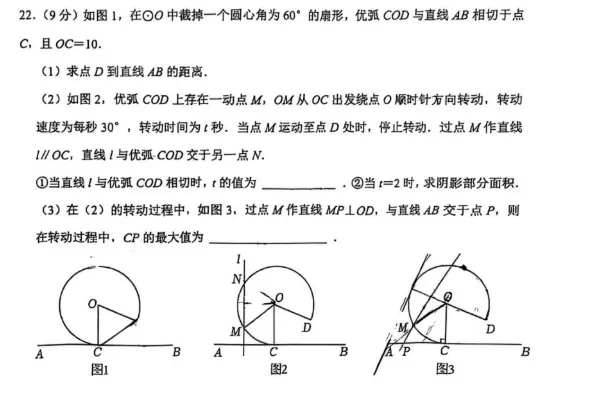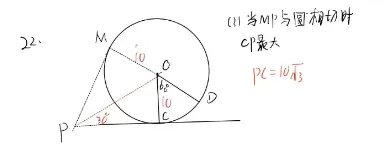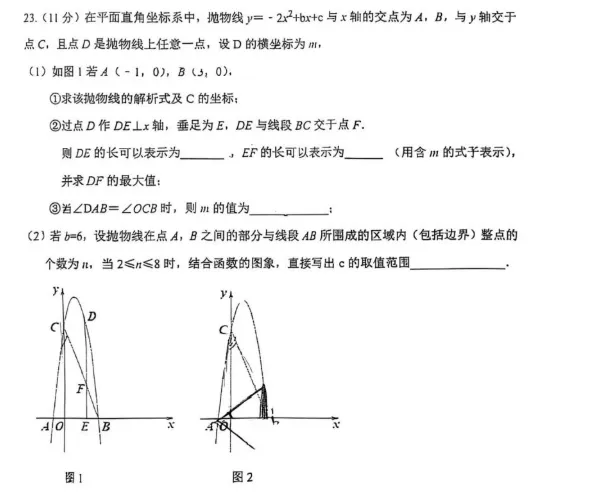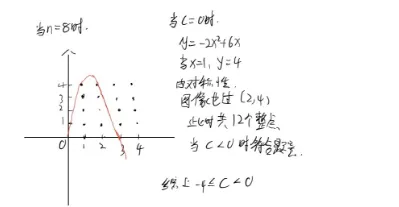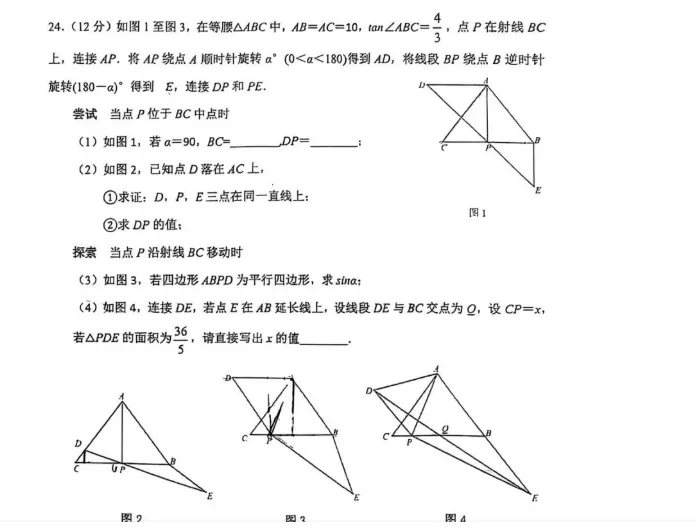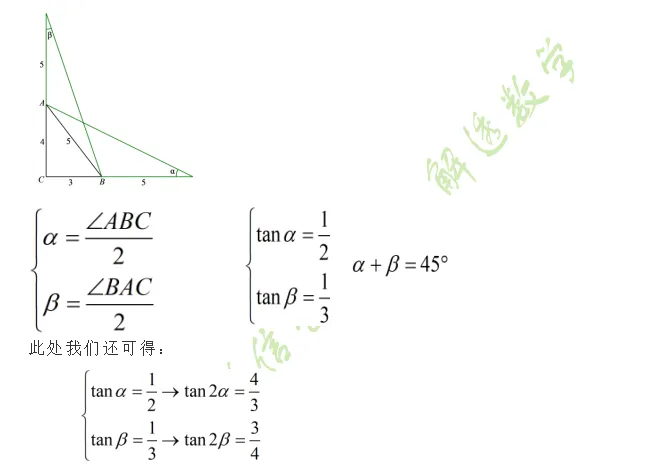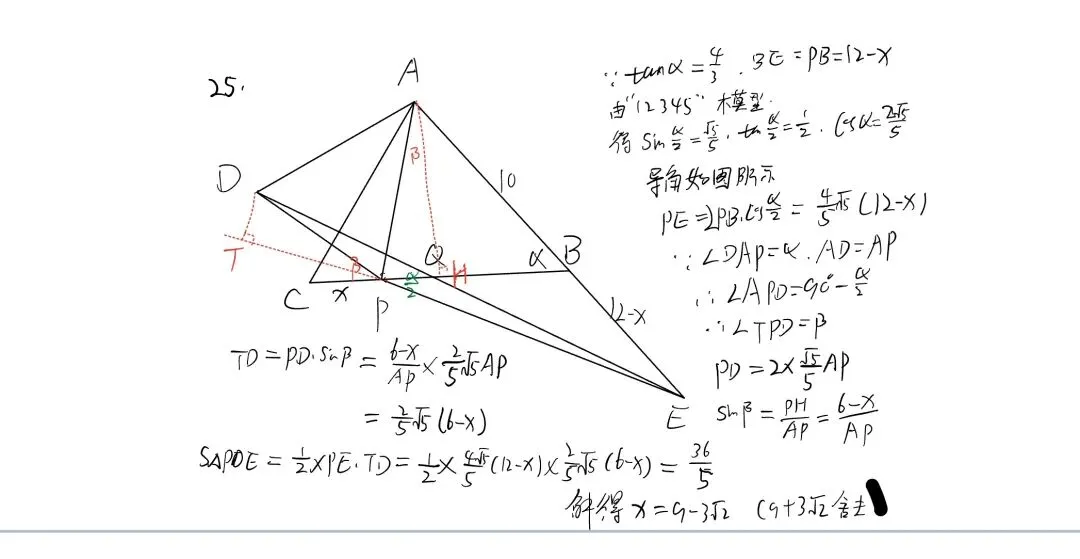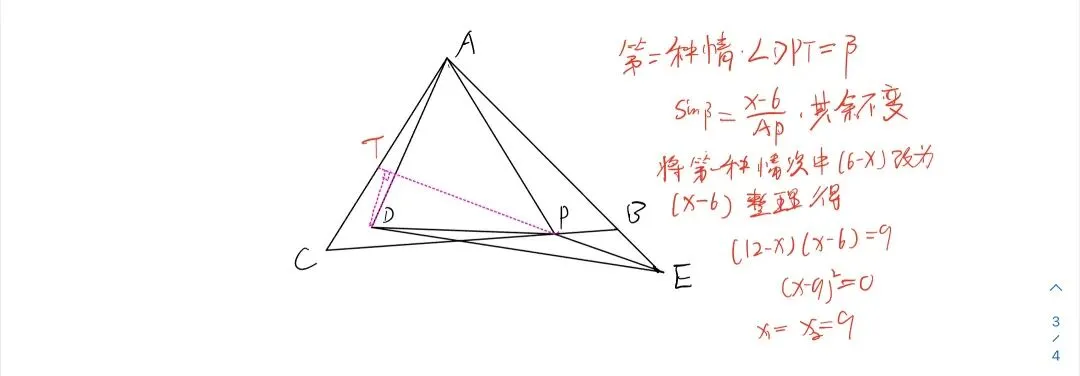本文来自网友投稿或网络内容，如有侵犯您的权益请联系我们删除，联系邮箱：wyl860211@qq.com 。

明天看谁真正七进七出,常山UUGvs石家庄WLT王者峡谷赵子龙之争!

邢台信都、襄都两区教育局最新发布...

最新文章

随机文章

基本 文件 流程 错误 SQL 调试
  1. 请求信息 : 2026-02-09 00:02:38 HTTP/2.0 GET : https://460.net.cn/a/468226.html
  2. 运行时间 : 0.173483s [ 吞吐率：5.76req/s ] 内存消耗：4,379.03kb 文件加载：140
  3. 缓存信息 : 0 reads,0 writes
  4. 会话信息 : SESSION_ID=00e1e6371d60a3f37a801f29495447b8
  1. /yingpanguazai/ssd/ssd1/www/460.net.cn/public/index.php ( 0.79 KB )
  2. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/autoload.php ( 0.17 KB )
  3. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/composer/autoload_real.php ( 2.49 KB )
  4. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/composer/platform_check.php ( 0.90 KB )
  5. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/composer/ClassLoader.php ( 14.03 KB )
  6. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/composer/autoload_static.php ( 4.90 KB )
  7. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-helper/src/helper.php ( 8.34 KB )
  8. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-validate/src/helper.php ( 2.19 KB )
  9. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/helper.php ( 1.47 KB )
  10. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/stubs/load_stubs.php ( 0.16 KB )
  11. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Exception.php ( 1.69 KB )
  12. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-container/src/Facade.php ( 2.71 KB )
  13. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/symfony/deprecation-contracts/function.php ( 0.99 KB )
  14. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/symfony/polyfill-mbstring/bootstrap.php ( 8.26 KB )
  15. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/symfony/polyfill-mbstring/bootstrap80.php ( 9.78 KB )
  16. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/symfony/var-dumper/Resources/functions/dump.php ( 1.49 KB )
  17. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-dumper/src/helper.php ( 0.18 KB )
  18. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/symfony/var-dumper/VarDumper.php ( 4.30 KB )
  19. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/App.php ( 15.30 KB )
  20. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-container/src/Container.php ( 15.76 KB )
  21. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/psr/container/src/ContainerInterface.php ( 1.02 KB )
  22. /yingpanguazai/ssd/ssd1/www/460.net.cn/app/provider.php ( 0.19 KB )
  23. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Http.php ( 6.04 KB )
  24. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-helper/src/helper/Str.php ( 7.29 KB )
  25. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Env.php ( 4.68 KB )
  26. /yingpanguazai/ssd/ssd1/www/460.net.cn/app/common.php ( 0.03 KB )
  27. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/helper.php ( 18.78 KB )
  28. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Config.php ( 5.54 KB )
  29. /yingpanguazai/ssd/ssd1/www/460.net.cn/config/app.php ( 0.95 KB )
  30. /yingpanguazai/ssd/ssd1/www/460.net.cn/config/cache.php ( 0.78 KB )
  31. /yingpanguazai/ssd/ssd1/www/460.net.cn/config/console.php ( 0.23 KB )
  32. /yingpanguazai/ssd/ssd1/www/460.net.cn/config/cookie.php ( 0.56 KB )
  33. /yingpanguazai/ssd/ssd1/www/460.net.cn/config/database.php ( 2.48 KB )
  34. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/facade/Env.php ( 1.67 KB )
  35. /yingpanguazai/ssd/ssd1/www/460.net.cn/config/filesystem.php ( 0.61 KB )
  36. /yingpanguazai/ssd/ssd1/www/460.net.cn/config/lang.php ( 0.91 KB )
  37. /yingpanguazai/ssd/ssd1/www/460.net.cn/config/log.php ( 1.35 KB )
  38. /yingpanguazai/ssd/ssd1/www/460.net.cn/config/middleware.php ( 0.19 KB )
  39. /yingpanguazai/ssd/ssd1/www/460.net.cn/config/route.php ( 1.89 KB )
  40. /yingpanguazai/ssd/ssd1/www/460.net.cn/config/session.php ( 0.57 KB )
  41. /yingpanguazai/ssd/ssd1/www/460.net.cn/config/trace.php ( 0.34 KB )
  42. /yingpanguazai/ssd/ssd1/www/460.net.cn/config/view.php ( 0.82 KB )
  43. /yingpanguazai/ssd/ssd1/www/460.net.cn/app/event.php ( 0.25 KB )
  44. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Event.php ( 7.67 KB )
  45. /yingpanguazai/ssd/ssd1/www/460.net.cn/app/service.php ( 0.13 KB )
  46. /yingpanguazai/ssd/ssd1/www/460.net.cn/app/AppService.php ( 0.26 KB )
  47. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Service.php ( 1.64 KB )
  48. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Lang.php ( 7.35 KB )
  49. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/lang/zh-cn.php ( 13.70 KB )
  50. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/initializer/Error.php ( 3.31 KB )
  51. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/initializer/RegisterService.php ( 1.33 KB )
  52. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/services.php ( 0.14 KB )
  53. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/service/PaginatorService.php ( 1.52 KB )
  54. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/service/ValidateService.php ( 0.99 KB )
  55. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/service/ModelService.php ( 2.04 KB )
  56. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-trace/src/Service.php ( 0.77 KB )
  57. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Middleware.php ( 6.72 KB )
  58. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/initializer/BootService.php ( 0.77 KB )
  59. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/Paginator.php ( 11.86 KB )
  60. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-validate/src/Validate.php ( 63.20 KB )
  61. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/Model.php ( 23.55 KB )
  62. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/model/concern/Attribute.php ( 21.05 KB )
  63. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/model/concern/AutoWriteData.php ( 4.21 KB )
  64. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/model/concern/Conversion.php ( 6.44 KB )
  65. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/model/concern/DbConnect.php ( 5.16 KB )
  66. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/model/concern/ModelEvent.php ( 2.33 KB )
  67. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/model/concern/RelationShip.php ( 28.29 KB )
  68. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-helper/src/contract/Arrayable.php ( 0.09 KB )
  69. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-helper/src/contract/Jsonable.php ( 0.13 KB )
  70. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/model/contract/Modelable.php ( 0.09 KB )
  71. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Db.php ( 2.88 KB )
  72. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/DbManager.php ( 8.52 KB )
  73. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Log.php ( 6.28 KB )
  74. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Manager.php ( 3.92 KB )
  75. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/psr/log/src/LoggerTrait.php ( 2.69 KB )
  76. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/psr/log/src/LoggerInterface.php ( 2.71 KB )
  77. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Cache.php ( 4.92 KB )
  78. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/psr/simple-cache/src/CacheInterface.php ( 4.71 KB )
  79. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-helper/src/helper/Arr.php ( 16.63 KB )
  80. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/cache/driver/File.php ( 7.84 KB )
  81. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/cache/Driver.php ( 9.03 KB )
  82. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/contract/CacheHandlerInterface.php ( 1.99 KB )
  83. /yingpanguazai/ssd/ssd1/www/460.net.cn/app/Request.php ( 0.09 KB )
  84. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Request.php ( 55.78 KB )
  85. /yingpanguazai/ssd/ssd1/www/460.net.cn/app/middleware.php ( 0.25 KB )
  86. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Pipeline.php ( 2.61 KB )
  87. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-trace/src/TraceDebug.php ( 3.40 KB )
  88. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/middleware/SessionInit.php ( 1.94 KB )
  89. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Session.php ( 1.80 KB )
  90. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/session/driver/File.php ( 6.27 KB )
  91. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/contract/SessionHandlerInterface.php ( 0.87 KB )
  92. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/session/Store.php ( 7.12 KB )
  93. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Route.php ( 23.73 KB )
  94. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/route/RuleName.php ( 5.75 KB )
  95. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/route/Domain.php ( 2.53 KB )
  96. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/route/RuleGroup.php ( 22.43 KB )
  97. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/route/Rule.php ( 26.95 KB )
  98. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/route/RuleItem.php ( 9.78 KB )
  99. /yingpanguazai/ssd/ssd1/www/460.net.cn/route/app.php ( 1.72 KB )
  100. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/facade/Route.php ( 4.70 KB )
  101. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/route/dispatch/Controller.php ( 4.74 KB )
  102. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/route/Dispatch.php ( 10.44 KB )
  103. /yingpanguazai/ssd/ssd1/www/460.net.cn/app/controller/Index.php ( 4.81 KB )
  104. /yingpanguazai/ssd/ssd1/www/460.net.cn/app/BaseController.php ( 2.05 KB )
  105. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/facade/Db.php ( 0.93 KB )
  106. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/connector/Mysql.php ( 5.44 KB )
  107. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/PDOConnection.php ( 52.47 KB )
  108. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/Connection.php ( 8.39 KB )
  109. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/ConnectionInterface.php ( 4.57 KB )
  110. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/builder/Mysql.php ( 16.58 KB )
  111. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/Builder.php ( 24.06 KB )
  112. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/BaseBuilder.php ( 27.50 KB )
  113. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/Query.php ( 15.71 KB )
  114. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/BaseQuery.php ( 45.13 KB )
  115. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/concern/TimeFieldQuery.php ( 7.43 KB )
  116. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/concern/AggregateQuery.php ( 3.26 KB )
  117. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/concern/ModelRelationQuery.php ( 20.07 KB )
  118. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/concern/ParamsBind.php ( 3.66 KB )
  119. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/concern/ResultOperation.php ( 7.01 KB )
  120. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/concern/WhereQuery.php ( 19.37 KB )
  121. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/concern/JoinAndViewQuery.php ( 7.11 KB )
  122. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/concern/TableFieldInfo.php ( 2.63 KB )
  123. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-orm/src/db/concern/Transaction.php ( 2.77 KB )
  124. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/log/driver/File.php ( 5.96 KB )
  125. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/contract/LogHandlerInterface.php ( 0.86 KB )
  126. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/log/Channel.php ( 3.89 KB )
  127. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/event/LogRecord.php ( 1.02 KB )
  128. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-helper/src/Collection.php ( 16.47 KB )
  129. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/facade/View.php ( 1.70 KB )
  130. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/View.php ( 4.39 KB )
  131. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Response.php ( 8.81 KB )
  132. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/response/View.php ( 3.29 KB )
  133. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/Cookie.php ( 6.06 KB )
  134. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-view/src/Think.php ( 8.38 KB )
  135. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/framework/src/think/contract/TemplateHandlerInterface.php ( 1.60 KB )
  136. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-template/src/Template.php ( 46.61 KB )
  137. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-template/src/template/driver/File.php ( 2.41 KB )
  138. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-template/src/template/contract/DriverInterface.php ( 0.86 KB )
  139. /yingpanguazai/ssd/ssd1/www/460.net.cn/runtime/temp/ba54d6633e0eed0ab3340e5f5fbe5cd0.php ( 11.97 KB )
  140. /yingpanguazai/ssd/ssd1/www/460.net.cn/vendor/topthink/think-trace/src/Html.php ( 4.42 KB )
  1. CONNECT:[ UseTime:0.000846s ] mysql:host=127.0.0.1;port=3306;dbname=nowww460;charset=utf8mb4
  2. SHOW FULL COLUMNS FROM `fenlei` [ RunTime:0.001604s ]
  3. SELECT * FROM `fenlei` WHERE `fid` = 0 [ RunTime:0.000688s ]
  4. SELECT * FROM `fenlei` WHERE `fid` = 63 [ RunTime:0.011846s ]
  5. SHOW FULL COLUMNS FROM `set` [ RunTime:0.001399s ]
  6. SELECT * FROM `set` [ RunTime:0.000616s ]
  7. SHOW FULL COLUMNS FROM `article` [ RunTime:0.001486s ]
  8. SELECT * FROM `article` WHERE `id` = 468226 LIMIT 1 [ RunTime:0.002937s ]
  9. UPDATE `article` SET `lasttime` = 1770566558 WHERE `id` = 468226 [ RunTime:0.023290s ]
  10. SELECT * FROM `fenlei` WHERE `id` = 65 LIMIT 1 [ RunTime:0.000800s ]
  11. SELECT * FROM `article` WHERE `id` < 468226 ORDER BY `id` DESC LIMIT 1 [ RunTime:0.001357s ]
  12. SELECT * FROM `article` WHERE `id` > 468226 ORDER BY `id` ASC LIMIT 1 [ RunTime:0.005053s ]
  13. SELECT * FROM `article` WHERE `id` < 468226 ORDER BY `id` DESC LIMIT 10 [ RunTime:0.002047s ]
  14. SELECT * FROM `article` WHERE `id` < 468226 ORDER BY `id` DESC LIMIT 10,10 [ RunTime:0.014292s ]
  15. SELECT * FROM `article` WHERE `id` < 468226 ORDER BY `id` DESC LIMIT 20,10 [ RunTime:0.009184s ]
0.179883s