n

2022~2023学年度第一学期期末八年级数学质量检测试题
一.选择题(每题3分,共48分)
1.数9的算术平方根是( )
A.±3B.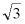 C.﹣3D.3
C.﹣3D.3
 2.代数式
2.代数式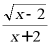 在实数范围内有意义,则x的值可能为( )
在实数范围内有意义,则x的值可能为( )
A.2B.0C.﹣2D.﹣1
3.围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.
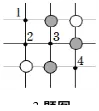
如图,黑白棋子摆成的图案里下一黑棋,要使棋子构成的图形既是
 轴对称图形也是中心对称图形,则黑棋落在( )号位置上
轴对称图形也是中心对称图形,则黑棋落在( )号位置上
A.4B.3C.2D.1
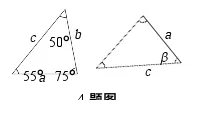
4.如图所示,两个三角形全等,则∠β等于( )
A.75°B.55°C.50°D.45°
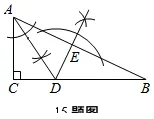
5.在实数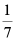
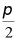 ,1.12112111211112…(每两个2之间依次多一个1)中,无理数的个数为( )
,1.12112111211112…(每两个2之间依次多一个1)中,无理数的个数为( )
A.2B.3C.4D.5
6.下列分式变形正确的是( )
 A.
A.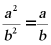 B.
B.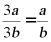 C.
C.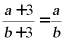 D.
D.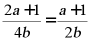
7.如图,数轴上点P表示的数可能是( )
A.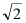 B.
B.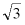 C.
C.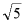 D.
D.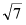
8.用反证法证明命题:“在△ABC中,∠A≠∠B,则AC≠BC”.应先假设()
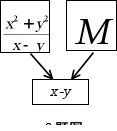 A.AC>BCB.AC<BCC.∠A=∠BD.AC=BC
A.AC>BCB.AC<BCC.∠A=∠BD.AC=BC
9.如图,若约定:上方相邻两个代数式之和等于两个代数式下方
箭头共同指向的代数式,则代数式M是 ()
 A.
A.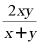 B.
B.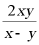 C.
C.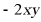 D.
D.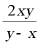
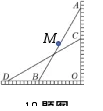
10.如图,一架梯子AB斜靠在竖直墙上,点M为梯子AB的中点,当梯子
底端向左水平滑动到CD位置时,滑动过程中OM的变化规律是()
A.变小B.不变C.变大D.先变小再变大
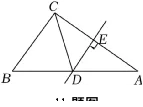 11.如图,直线DE是△ABC边AC的垂直平分线,且与AC相交于点E,与AB相交于点D,连接CD,已知BC=12cm,AB=16cm,则△BCD的周长为( )
11.如图,直线DE是△ABC边AC的垂直平分线,且与AC相交于点E,与AB相交于点D,连接CD,已知BC=12cm,AB=16cm,则△BCD的周长为( )
A.28cmB.22cmC.20cmD.18cm
12.满足下列条件时,△ABC不是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5B.∠A=2∠B=2∠C
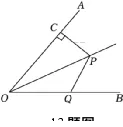 C.AB=
C.AB=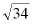 =3,AC=5D.∠A=20°,∠B=70°
=3,AC=5D.∠A=20°,∠B=70°
13.如图,点P在∠AOB的角平分线上,点P到OA边的距离等于5,
点Q是OB边上的任意一点,下列选项正确的是( )
A.PQ≤5B.PQ≥5C.PQ<5D.PQ>5
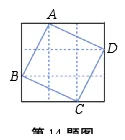 14.如图是3×3的正方形网格, 每一个小正方形的边长为1.
14.如图是3×3的正方形网格, 每一个小正方形的边长为1.
关于图中的正方形ABCD的面积S,三人的说法如下:
甲:要求面积S的值,必须先求出正方形ABCD的边长才行.
乙:正方形ABCD的边长是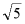 .
.
丙:正方形ABCD的对角线长m的值介于整数3和4之间.
下列判断正确的是()
A.甲、乙、丙都对B.甲和乙对C.甲、乙、丙都不对D. 乙和丙对
 15.如图,在Rt△ABC中,∠ACB=90°,根据尺规作图的痕迹,判断以下结论错误的是( )
15.如图,在Rt△ABC中,∠ACB=90°,根据尺规作图的痕迹,判断以下结论错误的是( )
A. DE=DCB. AE=ACC. AD=BDD.∠BDE=∠BAC
16.如图,是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是3,4,5,6,9选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
 A.5,6,9B.4,5,9C.3,4,5D.3,3,6
A.5,6,9B.4,5,9C.3,4,5D.3,3,6
二、 填空题(3×5=15分)
填空题(3×5=15分)
17.(1)请写出“对顶角相等”这一命题的逆命题.
(2)如图,校园内的一块草坪是长方形ABCD,已知AB=8m,BC=6m,从A点到C点,
同学们为了抄近路,常沿线段AC走,那么同学们少走了m.
(3)已知等腰三角形的两边长分别为a、b,且a、b满足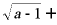 |b﹣3|=0,则此等腰
|b﹣3|=0,则此等腰
三角形的周长为.
(4)如图,在△ABC中,∠C=90°,∠A=30°,AB=6cm,动点P、Q同时从A、B
两点出发,分别在AB、BC边上匀速移动,它们的速度分别为VP=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点同时停止运动,设点P的运动时间为ts.
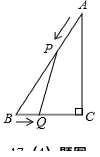 ①当t=秒时,△PBQ为等边三角形;
①当t=秒时,△PBQ为等边三角形;
②当t=秒时,△PBQ为直角三角形.
三、解答题
18.(18分)完成下列各题:
 (1)计算:
(1)计算: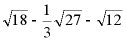 ;
;
(2)计算: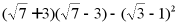
 (3)解方程:
(3)解方程: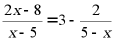
19.(8分)先化简,再求值:当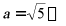 分式
分式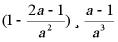 的值
的值
20.(10分)如图,AC=MN,∠1=∠2,∠A=∠M,点N在线段AC上.
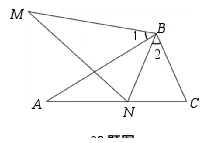 (1)求证:△ABC≌△MBN;
(1)求证:△ABC≌△MBN;
(2)若∠1=50°,求∠ANB的度数.
21.(10分)某学校在某药店购买84消毒液和口罩 ,购买84消毒液共花费900元,购买口罩共花费2160元,购买口罩数量(单位:包)是购买84消毒液数量(单位:瓶)的2倍,且购买一包口罩比购买一瓶84消毒液多花1元.
(1)求购买一瓶84消毒液和一包口罩的单价各是多少元;
(2)按照实际需要每个班须配备84消毒液3瓶,口罩6包用于防疫,则购买的84消毒液和口罩能够配备多少个班级?
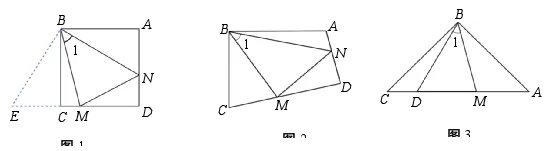 22.(11分)探究:如图1和图2,四边形ABCD中,已知AB=BC,∠ABC=90°,点M、N分别在CD、AD上,∠1=45°.
22.(11分)探究:如图1和图2,四边形ABCD中,已知AB=BC,∠ABC=90°,点M、N分别在CD、AD上,∠1=45°.
(1)①如图1,若∠A、∠C都是直角,把△BAN绕点B顺时针旋转90°至△BCE,使AB
与BC重合,直接写出线段AN、CM和MN之间的数量关系_____________________;
②如图2,若∠A、∠C都不是直角,但满足∠A+∠C=180°,线段AN、CM和MN之间的结论是否仍然成立,若成立,请写出证明过程,若不成立,请说明理由.
(2)拓展:如图3,在△ABC中,∠CBA=90°,BC=BA=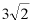 D、M均在边AC边上,
D、M均在边AC边上,
且∠1=45°,若CD=2,请直接写出DM的长.

通过网盘分享的文件:试卷1
链接: https://pan.baidu.com/s/1982iMYRRt5d5rlVaKpTarQ?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享